Communication-Avoiding Algorithms, Part 1: Why Avoid Communication?

This is part 1 of an ongoing sequence of posts on communication-avoiding algorithms. This page will be updated with a link to the next page when it’s posted.

If you’ve played around with algorithms before, you’ve probably seen complexity metrics that measure how many boolean or arithmetic operations an operation does. Classic examples include things like finding optimal sorting algorithms (e.g. those of you who have taken a data structures class will probably have seen O(nlog n) lower bound for sorting and a proof that Quicksort attains this cost).

Unfortunately, the picture isn’t so simple in real life, and computational costs often aren’t the limiting factor in terms of performance. To get an idea of why this might be the case, let’s take a look at the specs for a modern CPU such as this Intel Ice Lake chip from 2019:

L1 Data Cache Latency = 5 cycles for simple access via pointer

L1 Data Cache Latency = 5 cycles for access with complex address calculation (size_t n, *p; n = p[n]).

L2 Cache Latency = 13 cycles

L3 Cache Latency = 42 cycles (core 0)

RAM Latency = 42 cycles + 87 ns

In other words, even if your data is already in cache, asking for something in memory means waiting between five and forty-two cycles for the data to get back to you. Even if you know exactly what memory accesses need you’ll need next, communication often still ends up eating up the majority of the time and energy spent computing something. For instance, this paper provides some energy cost breakdowns for neural net accelerators. As the following diagram shows, memory accesses to the on-chip buffer dominate the total cost.

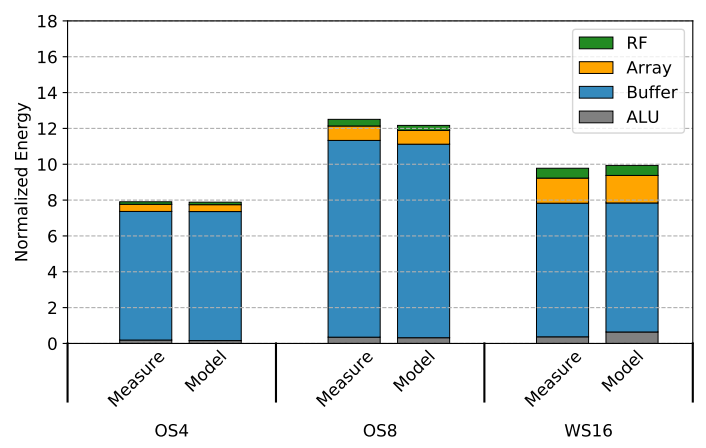
The situation gets even worse if you have to go off-chip: Nvidia’s Bill Dally estimates that accessing a bit of off-chip memory costs between five and twenty-eight times as much as accessing a bit of local on-chip memory.

Looking at hardware trends, the picture gets even worse - the cost of memory accesses, compared to arithmetic operations, is increasing over time, despite fact that the rate of improvement in arithmetic processing has shrunk over time thanks to the end of Moore’s law.

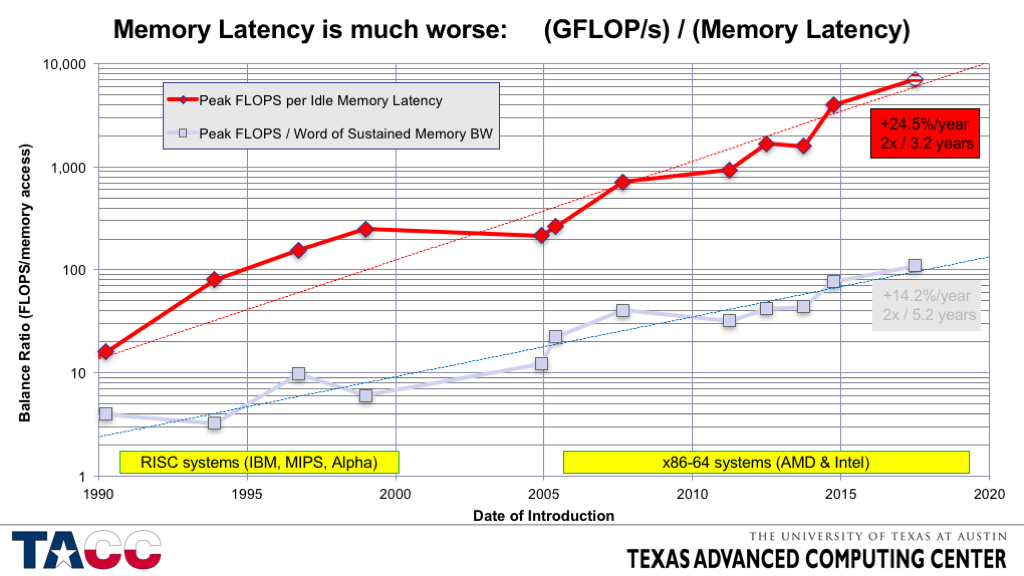
The key takeaways are that if we want good performance, we need to minimize communication, both between the chip and the rest of the system (whether that means memory or other chips in a multiprocessor system) and within elements of a chip. Algorithms that do this are known as communication-avoiding algorithms, and since data movement is so critical to obtaining maximal performance, they actually turn up everywhere, hidden behind the scenes in highly optimized libraries that all sorts of programs call directly or indirectly. A few notable examples:

• All the standard linear algebra libraries such as Intel’s MKL

• Fast Fourier transforms are a heavily used computational kernel with applicatons in signal processing, image and video decoding and encoding (underlying both JPEG and MP3 formats), and numerical analysis. Library implementations such as the classic FFTW and later implementations by multiple subsequent industry vendors have explicitly leveraged algorithmic techniques to reduce computation and boost performance.

• Training deep nets, which produces the models that you run on your phone every time you log in with Face ID, often heavily comm

• Performing inference on neural nets is often communication-bound, as shown in the first figure in this article. As a result... and inference accelerators heavily

We’ll discuss the principles behind some techniques used to reduce communication in this series. There are a few methods we’ll consider:

One way to approach this problem is autotuning - trying a lot of different the

For a lot of problems, this works quite well, and there are several projects and successful companies in the space.

However, this has

Fortunately, data movement is one of the few metrics that we can find lower bounds on - that is, we can mathematically prove statements explicitly quantifying the minimum amount of data movement required to perform some operation. These statements often correspond to algorithms (and in fact, the techniques used to prove these lower bounds often are related to the techniques used to find algorithms that actually attain them, so we’ll also cover some techniques for finding communication lower bounds.

References